法线变换矩阵
经过模型变换后，法线也要跟着一起变换。假设物体发生了缩放形变，如果对法线应用相同的变换，可能会得到错误结果：
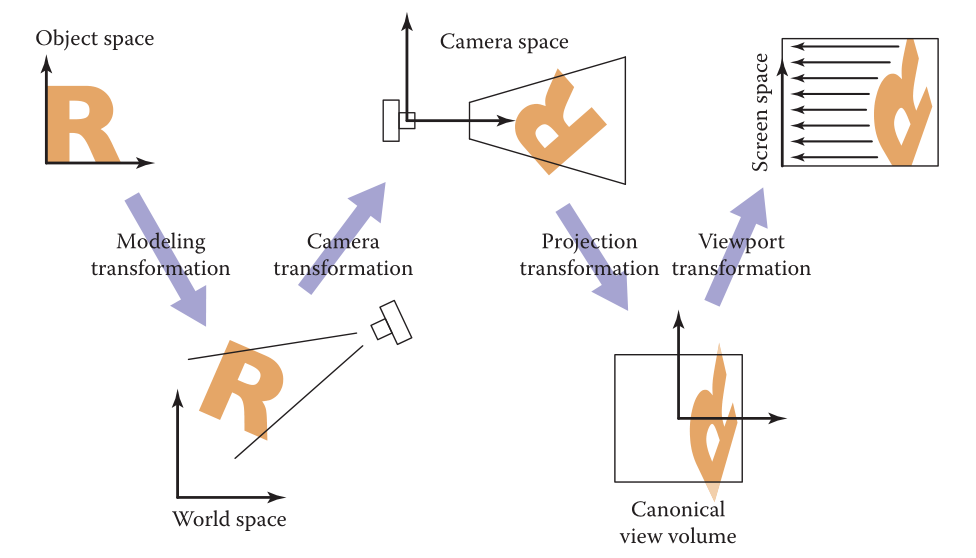
物体在呈现在屏幕前，要经过一系列的变换。前三步（Modeling transformation、Camera transformation、Projection transformation）都由我们自己完成，最后一步由显卡完成（包括裁剪、Viewport transformation、光栅化等步骤）。前三步也称为MVP变换。
下文均是建立在右手坐标系，相机朝向z轴负方向。
一、三角形光栅化
三角形光栅化就是将三角面片覆盖的像素绘制出来，从而在屏幕上可见。有几个目标需要实现：
不重复的：不重复绘制像素，例如相邻的三角形之间公共边覆盖到的像素应当只被绘制一次。
无缝的：例如相邻的三角形之间光栅化出来应当是没有缝隙的，连续的。
2D平面中三角形
对于2D空间三角形，假设三个顶点分别为\(\mathbf{a} ,\mathbf{b},\mathbf{c}\)。则2D空间任意点都可以被下式表示出来：
\[ \mathbf{p}=\mathbf{a}+\beta(\mathbf{b}-\mathbf{a})+\gamma(\mathbf{c}-\mathbf{a})\tag{1} \]
可以理解为\(\mathbf{a}\)为起点，向量\((\mathbf{b}-\mathbf{a})\)和\((\mathbf{c}-\mathbf{a})\)构成的基张成一个平面空间。
在介绍旋转之前，先分析一下两个概念：旋转和方向。方向即一个单位向量；旋转用来描述一个方向如何变换到另一个方向。在3维空间中，使一个方向变换到另一个方向的旋转有无数种，因为变换后的向量还可以绕以自己为旋转轴轴旋转。这意味着将旋转说成是一个方向变换到另一个方向的过程是不严谨的。准确地说，旋转描述的是坐标系到坐标系的变换。在3维空间中，只知道一个方向会变换到另一个方向，是无法唯一确定一个旋转的（当然也是可以构造出满足条件的旋转的，比如指定一个上向量）。
概述
C/C++ 编译流程： 编译、汇编、链接
在汇编完成后，会生成中间文件。windows下是.obj，Unix下是.o。
编译时，只要源代码的语法正确，编译器就可以编译出中间目标文件。
链接时，主要是链接函数和全局变量。所以，我们可以使用这些中间目标文件（ .o 文件或 .obj 文件）来链接我们的应用程序。在大多数时候，由于源文件太多，编译生成的中间目标文件太多，而在链接时需要明显地指出中间目标文件名，这对于编译很不方便。所以，我们要给中间目标文件打个包，在Windows下这种包叫“库文件”（Library File），也就是 .lib 文件，在UNIX下，是Archive File，也就是 .a 文件。
参考
基本就是下面的教程的搬运+一点的自己理解
学习OpenGL的过程中想要实现一些效果，遇到的坑和找到的解决方案，记录一下。
先看看C++ Primer的解释：
C++的表达式要不然是右值，要不然就是左值。这两个名词是从C语言继承过来的，原本是为了帮助记忆：左值可以位于赋值语句的左侧，右值则不能。
在C++语言中，二者的区别就没那么简单了。一个左值表达式的求值结果是一个对象或者一个函数，然而以常量对象为代表的某些左值实际上是不能作为赋值语句的左侧运算对象。此外，虽然某些表达式的求值结果是对象，但它们是右值而非左值。可以做一个简单的归纳；当一个对象被用作右值的时候，用的是对象的值（内容）；当对象被用作左值的时候，用的是对象的身份（在内存中的位置）。
使用关键字
decltype的时候，左值和右值也有所不同。如果表达式的求值结果是左值，decltype作用于该表达式（不是变量）得到一个引用类型。举个例子，假定p的类型是int*，因为解引用运算符生成左值，所以decltype(*p)的结果是int&。另一方面，因为取地址运算符生成右值，所以decltype(&p)的结果int**，也就是说，结果过是一个指向整数指针的指针。